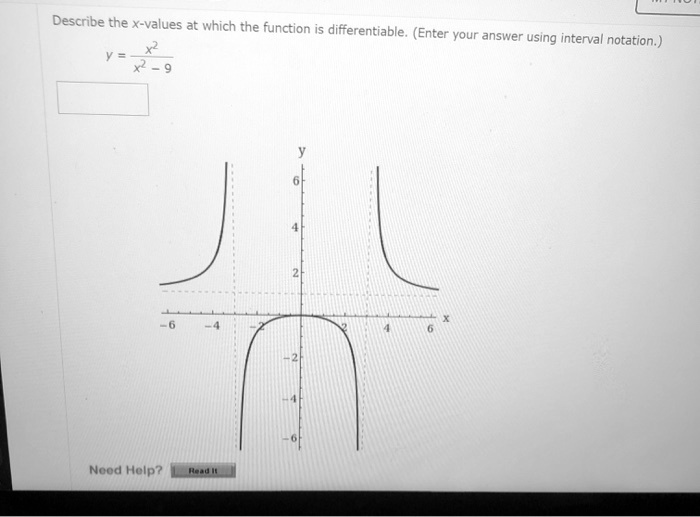
Describe The X Values At Which The Function Is Differentiable . Briefly, differentiable means can be differentiated and that mean has a derivative. Function g below is not differentiable at x = 0 because there is no tangent to the graph at x = 0.(try to draw a tangent at x=0!) function h below is not differentiable at x = 0 because there is a jump in the value of the function and also the function is not defined therefore not continuous at x = 0.
Solved Describe The X-Values At Which The Function Is | Chegg.com from www.chegg.com
At x=0 the function is not defined so it makes no sense to ask if they are differentiable there. The verb, differentiate means find the derivative.
Solved Describe The X-Values At Which The Function Is | Chegg.com
Hence, |x| is not differentiable at x=0. More generally, a function is said to be differentiable on if it is differentiable at every point in an open set , and a differentiable function is one in. To be differentiable at a certain point, the function must first of all be defined there!
Source: www.numerade.com
As we head towards x = 0 the function moves up and down faster and faster, so we cannot find a value it is heading towards. For example, the function f ( x) = 1 x only makes sense for values of x that are not equal to zero. So this looks like we are both continuous and differentiable.
Source: www.chegg.com
At point c c c on the interval [a, b] [a, b] [a, b] of the function f (x) f(x) f (x), where the function is. At x=0 the function is not defined so it makes no sense to ask if they are differentiable there. Function j below is not differentiable at x.
Source: www.chegg.com
Hence the function f (x) = ∣∣x2 − 9∣∣ is differentiable everywhere with the exception of x = ± 3. (enter your answer using interval notation. A function f f f is differentiable at a point x 0 x_0 x 0 if.
Source: www.bartleby.com
F ′ ( x) = lim δ x → 0 f ( x + δ x) − f ( x) δ x for x ≤ 0: Although x2 −9 is both continuous and differentiable everywhere the same is not true for ∣∣x2 −9∣∣, which is continuous everywhere but not differentiable at the transition between positive and negative. As in.
Source: study.com
Definition function f is differentiable at x=a if and only if f'(a) exists. But for modulus function at x=0, no unique tangent can be drawn. Otherwise, it's not differentiable at x=a.
Source: www.chegg.com
A function is said to be differentiable at x=a, if a unique tangent passes through that point. F ′ ( x) f' (x) f ′ ( x) using the limit definition. F ′ ( x) = lim δ x → 0 f ( x + δ x) − f ( x) δ x for x ≤ 0:
Source: www.numerade.com
Hence the function f (x) = ∣∣x2 − 9∣∣ is differentiable everywhere with the exception of x = ± 3. The noun differentiation is the act or process of differentiating, hence, the act or process of finding a derivative. Briefly, differentiable means can be differentiated and that mean has a derivative.
Source: www.chegg.com
(enter your answer using interval notation. So it looks like our derivative exists there, and it is equal to limit as x approaches three of all of this because this is equal to six, because the limit is approached from the left and the right is also equal to six. Although x2 −9 is both continuous and differentiable everywhere the.
Source: www.chegg.com
The derivative function, denoted by , is the function whose domain consists of those values of such that the following limit exists: (enter your answer using interval notation. 1) f f f is continuous at x 0 x_0 x 0 and 2) the slope of tangent at point x 0 x_0 x 0 is well defined.
Source: www.chegg.com
F(x) is differentiable everywhere except at x = 0. Otherwise, it's not differentiable at x=a. The function is differentiable for all x + +8.
Source: www.chegg.com
Its domain is the set { x ∈ r: Piecewise functions may or may not be differentiable on their domains. So this looks like we are both continuous and differentiable.
Source: www.bartleby.com
A function f f f is differentiable at a point x 0 x_0 x 0 if. To be differentiable at a certain point, the function must first of all be defined there! Although x2 −9 is both continuous and differentiable everywhere the same is not true for ∣∣x2 −9∣∣, which is continuous everywhere but not differentiable at the transition between.
Source: www.chegg.com
The noun differentiation is the act or process of differentiating, hence, the act or process of finding a derivative. Briefly, differentiable means can be differentiated and that mean has a derivative. Hence, |x| is not differentiable at x=0.
Source: www.chegg.com
The function is differentiable for all x + +8. At point c c c on the interval [a, b] [a, b] [a, b] of the function f (x) f(x) f (x), where the function is. A function is said to be differentiable at if.
Source: www.bartleby.com
Let’s consider some piecewise functions first. The function is differentiable for all x # +64. At x=0 the function is not defined so it makes no sense to ask if they are differentiable there.
Source: www.chegg.com
1) f f f is continuous at x 0 x_0 x 0 and 2) the slope of tangent at point x 0 x_0 x 0 is well defined. (enter your answer using interval notation. At x=0 the function is not defined so it makes no sense to ask if they are differentiable there.
Source: www.bartleby.com
Piecewise functions may or may not be differentiable on their domains. So this looks like we are both continuous and differentiable. F ′ ( x) f' (x) f ′ ( x) using the limit definition.
Source: www.bartleby.com
At point c c c on the interval [a, b] [a, b] [a, b] of the function f (x) f(x) f (x), where the function is. Otherwise, it's not differentiable at x=a. In other words, it's the set of all real numbers that are not equal to zero.
Source: itprospt.com
F(x) is differentiable on the interval (2, infinity). So it looks like our derivative exists there, and it is equal to limit as x approaches three of all of this because this is equal to six, because the limit is approached from the left and the right is also equal to six. F ′ ( x) = lim δ.
Source: www.numerade.com
Hence, |x| is not differentiable at x=0. Let’s consider some piecewise functions first. Definition function f is differentiable at x=a if and only if f'(a) exists.